4030. Идол
Карл принимает
участие в предварительном раунде Шоу Талантов под названием Северо-Западный
Европейский Идол (СЗЕИ) и хочет попасть в следующий раунд: Мировой Идол. В Шоу
Талантов у каждого участника имеется 10 минут, чтобы произвести впечатление на
судей. После выступления всех участников каждый судья примет два различных
решения. Судья может проголосовать либо в пользу участника (что означает его
проход в следующий раунд), либо против участника (что означает непопадание в
следующий раунд). Заранее неизвестно количество участников, которое попадет в
следующий раунд. Если все конкурсанты будут выступать очень плохо, то никто не
пройдет в следующий раунд. Либо если все выступления участников будут
восхитительными, то все они пройдут в следующий раунд.
Карл боится, что
судьи не оценят по достоинству его таланты программирования, поэтому он решает
использовать другие свои способности для попадания в следующий раунд: взлом.
Получив доступ к системе жюри, Карл способен переопределить официальный процесс
подсчета голосов, выбрав, какие именно участники перейдут к следующему раунду.
Единственная проблема в том, что он должен быть осторожным, чтобы не вызвать
подозрений.
Каждый судья
ожидает, что по крайней мере одно из его (или ее) собственных двух решений
будет соответствовать итогам конкурса. Если результат будет противоречить обоим
голосам, то судья поднимет тревогу. Например, пусть судья Гарри голосует в
пользу Пита и против Салли. Если Салли проходит в следующий раунд, а Пит нет,
то судья Гарри будет обеспокоен и может заподозрить Карла в манипуляции с
системой.
Так как Карл не
силен в программировании (в противном случае он бы не нуждался во взломе), он
хочет, чтобы Вы написали программу, которая определит, существует ли набор
участников, включающий и его самого, который он может выбрать для прохода в
следующий раунд путем взлома системы жюри так, что ни один из судей не
заподозрит его в этом.
Вход. Каждый тест состоит из:
·
первая строка содержит два натуральных числа: количество
участников n (2 ≤ n < 1000) и количество судей m (1 ≤ m < 2000).
·
m строк,
содержащих результаты голосования каждого судьи. В каждой из этих строк
находится два целых числа: a (1
≤ |a| ≤ n) и b
(1 ≤ |b| ≤ n) – результаты голосования судьи (|a| ≠ |b|). Голос x < 0
означает решение против прохода участника |x|
в следующий раунд. Голос x > 0
означает решение за участника |x|.
Участники
пронумерованы от 1 до n. Карл имеет
номер участника 1.
Выход. Для каждого теста вывести в отдельной строке слово 'yes',
если существует множество участников, которое вместе с Карлом пройдет в
следующий раунд, при этом ни один из судей не поднимет тревогу. Если такого
множества участников нет, то следует вывести 'no'.
|
Пример
входа |
Пример
выхода |
|
4 3 1 2 -2 -3 2 4 2 4 1 2 1 -2 -1 2 -1 -2 |
yes no |
РЕШЕНИЕ
2-выполнимость
Анализ алгоритма
Поставим в соответствие каждому участнику переменную xi. Рассмотрим булеву формулу
в конъюнктивной нормальной форме, где каждый конъюнкт содержит в точности 2
дизъюнкта вида a Ú b для каждого
голосования судьи. Если судья голосует против участника, то переменная в
конъюнкт входит с отрицанием.
Далее следует проверить выполнимость построенной формулы при
условии, что x1 = 1 (Карл
проходит в следующий раунд).
Если в графе импликаций существует путь из x1 в ![]() , то имеет место
, то имеет место ![]() , что выполняется лишь при x1 = 0. То есть в таком случае решения не существует.
, что выполняется лишь при x1 = 0. То есть в таком случае решения не существует.
Пример
В первом тесте
имеется 4 участника и 3 судьи.
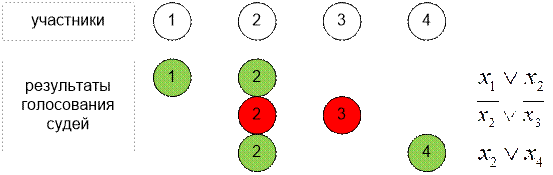
Следует
проверить на выполнимость формулу
![]()
при условии, что
x1 = 1 (Карл проходит в
следующий раунд).
Реализация алгоритма
Входной граф
храним в списке смежности g. Обратный граф (граф, в котором изменены все
направления ребер) храним списке смежности gr. Массив used используется для
отмечания уже пройденных вершин, top для топологической сортировки вершин, а
Color для покраски вершин согласно их вхождению в компоненты сильной связности.
vector<vector<int> > g, gr;
vector<int> used, top, Color;
Поиск в глубину
на входном графе. В массив top заносим последовательность вершин, в которой
поиск в глубину завершает их обработку.
void dfs1(int
v)
{
int i, to;
used[v] = 1;
for(i = 0; i
< g[v].size(); i++)
{
to = g[v][i];
if
(!used[to]) dfs1(to);
}
top.push_back(v);
}
Поиск в глубину на обратном графе.
Все вершины, которые будут пройдены в результате рекурсивного вызова функции
dfs2, принадлежат одной компоненте сильной связности. Красим все пройденные
вершины цветом с.
void dfs2(int
v, int c)
{
int i, to;
Color[v] = c;
for(i = 0; i
< gr[v].size(); i++)
{
to = gr[v][i];
if
(Color[to] == -1) dfs2(to,c);
}
}
Согласно импликативной связи u É v добавляем в
граф ребра (u, v) и (!v, !u).
void AddEdge(int
u, int v)
{
g[u].push_back(v); g[v^1].push_back(u^1);
gr[v].push_back(u); gr[u^1].push_back(v^1);
}
Основная часть
программы. Вершины входного графа нумеруются от 1 до n. Поскольку каждую вершину входного графа следует расщепить на
две, то поставим в соответствие вершине vi
входного графа вершины 2i – 2 и 2i – 1 в графе импликаций. Вершины графа
импликаций будут нумероваться с 0 до 2n
– 1, причем четным вершинам будут соответствовать вершины vi, а нечетным их отрицания !vi.
while(scanf("%d
%d",&n,&m) == 2)
{
g.assign(2*n,vector<int>());gr.assign(2*n,vector<int>());
for(i = 0; i
< m; i++)
{
scanf("%d
%d",&u,&v);
if (u >
0) u = 2 * u - 2; else u = (2 * (-u) - 2) ^ 1;
if (v >
0) v = 2 * v - 2; else v = (2 * (-v) - 2) ^ 1;
AddEdge(u^1, v);
}
Запустим поиск в глубину из вершины
0, которой соответствует переменная x1.
Вершине 1 соответствует переменная ![]() . Если по окончании поиска станет used[1] = 1, то существует
путь из 0 в 1 или имеет место импликация
. Если по окончании поиска станет used[1] = 1, то существует
путь из 0 в 1 или имеет место импликация ![]() . Для ее истинности необходимо выбрать x1 = 0. Поскольку Карлу соответствует переменная x1 и он должен пройти в
следующий раунд, то должно быть x1
= 1. То есть при used[1] = 1 Карл не сможет взломать систему.
. Для ее истинности необходимо выбрать x1 = 0. Поскольку Карлу соответствует переменная x1 и он должен пройти в
следующий раунд, то должно быть x1
= 1. То есть при used[1] = 1 Карл не сможет взломать систему.
top.clear();
used.assign(2*n,0);
dfs1(0);
if (used[1])
{
printf("no\n");
continue;
}
Запускаем поиск в глубину на графе
импликаций. Последовательность, в которой завершается обработка вершин графа,
сохраняется в массиве top.
top.clear();
used.assign(2*n,0);
for(i = 0; i
< 2*n; i++)
if
(!used[i]) dfs1(i);
Запускаем поиск в глубину на обратном
графе. Вершины обратного графа рассматриваем в порядке обхода массива top с
конца в начало. Вершины, входящие в одну компоненту сильной связности, красим
одним и тем же цветом. Текущий цвет раскраски находится в переменной с.
Color.assign(2*n,-1);
for(i = 0, c
= 0; i < 2*n; i++)
{
v = top[2*n-i-1];
if (Color[v] == -1) dfs2(v,c++);
}
Если некоторая переменная и ее
отрицание входят в одну сильно связную компоненту (соответствующие ей вершины i и i
XOR 1 покрашены одним цветом), то решения не существует.
for (flag = i
= 0; i < 2*n; i += 2)
if
(Color[i] == Color[i^1])
{
flag = 1; break;
}
В зависимости от значения flag выводим ответ.
printf("%s\n",
flag ? "no" : "yes");
}